Understanding BYOL: Bootstrap Your Own Latent for Self-Supervised Learning

In the realm of self-supervised learning, BYOL (Bootstrap Your Own Latent) has emerged as a groundbreaking method that challenges traditional paradigms. Unlike its predecessor, SimCLR, which relies on negative samples to learn representations, BYOL takes a different approach by focusing solely on positive pairs. This article delves into the intricacies of BYOL, its architecture, loss function, and its implications for self-supervised learning in computer vision.

What is BYOL?

BYOL is a self-supervised learning algorithm designed to learn image representations without the need for labeled data. The core idea behind BYOL is to minimize the distance between representations of the same image under different augmentations while avoiding the use of negative samples. This unique approach allows BYOL to operate effectively even with smaller batch sizes, making it a compelling choice for various applications.

Key Advantages of BYOL

1. No Negative Samples: BYOL eliminates the need for negative samples, which are often challenging to obtain and can complicate the training process. Instead, it focuses on maximizing the similarity between augmented views of the same image.

2. Smaller Batch Sizes: The absence of negative samples means that BYOL can achieve competitive performance with smaller batch sizes, which is particularly advantageous in scenarios where computational resources are limited.

The Architecture of BYOL

BYOL’s architecture consists of two main components: the online network (referred to as the "student") and the target network (referred to as the "teacher"). The student network is responsible for generating predictions, while the teacher network serves as a stable reference for learning.

Asymmetry in Architecture

One of the defining features of BYOL is its asymmetric architecture. The student network includes an additional Multi-Layer Perceptron (MLP) called the predictor, which is not present in the teacher network. This asymmetry is crucial for preventing mode collapse, a situation where the model outputs the same representation for all inputs.

The teacher network is updated using an exponential moving average (EMA) of the student’s parameters, ensuring that it remains a stable target throughout training. This process can be implemented as follows:

class EMA():
    def __init__(self, alpha):
        super().__init__()
        self.alpha = alpha

    def update_average(self, old, new):
        if old is None:
            return new
        return old * self.alpha + (1 - self.alpha) * new

ema = EMA(0.99)
for student_params, teacher_params in zip(student_model.parameters(), teacher_model.parameters()):
    old_weight, up_weight = teacher_params.data, student_params.data
    teacher_params.data = ema.update_average(old_weight, up_weight)

Loss Function

The loss function in BYOL is another critical aspect that differentiates it from other self-supervised methods. The predictor MLP is applied only to the student network, which helps avoid mode collapse. The authors of BYOL defined the loss as the mean squared error between the L2-normalized predictions and target projections:

[
\mathcal{L}{\theta, \xi} \triangleq \left|\bar{q}{\theta}\left(z{\theta}\right) – \bar{z}{\xi}^{\prime}\right|{2}^{2} = 2 – 2 \cdot \frac{\left\langle q{\theta}\left(z{\theta}\right), z{\xi}^{\prime}\right\rangle}{\left|q{\theta}\left(z{\theta}\right)\right|{2} \cdot \left|z{\xi}^{\prime}\right|_{2}}
]

This loss can be implemented in PyTorch as follows:

import torch
import torch.nn.functional as F

def loss_fn(x, y):
    x = F.normalize(x, dim=-1, p=2)
    y = F.normalize(y, dim=-1, p=2)
    return 2 - 2 * (x * y).sum(dim=-1)

Tracking Performance: KNN Accuracy

While the loss function provides insight into the training process, it is not always a reliable metric for evaluating self-supervised learning performance. A more effective method is to measure KNN (k-nearest neighbors) accuracy, which allows for a quick assessment of the learned representations without the need for a linear classifier.

The KNN implementation can be encapsulated in a class, enabling easy extraction of features and evaluation of accuracy:

import numpy as np
import torch
from sklearn.model_selection import cross_val_score
from sklearn.neighbors import KNeighborsClassifier

class KNN():
    def __init__(self, model, k, device):
        super(KNN, self).__init__()
        self.k = k
        self.device = device
        self.model = model.to(device)
        self.model.eval()

    def extract_features(self, loader):
        x_lst = []
        features = []
        label_lst = []
        with torch.no_grad():
            for input_tensor, label in loader:
                h = self.model(input_tensor.to(self.device))
                features.append(h)
                x_lst.append(input_tensor)
                label_lst.append(label)
            x_total = torch.stack(x_lst)
            h_total = torch.stack(features)
            label_total = torch.stack(label_lst)
            return x_total, h_total, label_total

    def knn(self, features, labels, k=1):
        feature_dim = features.shape[-1]
        with torch.no_grad():
            features_np = features.cpu().view(-1, feature_dim).numpy()
            labels_np = labels.cpu().view(-1).numpy()
            self.cls = KNeighborsClassifier(k, metric="cosine").fit(features_np, labels_np)
            acc = self.eval(features, labels)
        return acc

    def eval(self, features, labels):
        feature_dim = features.shape[-1]
        features = features.cpu().view(-1, feature_dim).numpy()
        labels = labels.cpu().view(-1).numpy()
        acc = 100 * np.mean(cross_val_score(self.cls, features, labels))
        return acc

Modifying ResNet for BYOL

To implement BYOL effectively, we can modify a base model, such as ResNet-18, by replacing the final classification layer with an identity function and adding MLP projection heads. This allows the output features to be fed into the MLP projector for further processing.

import copy
import torch
from torch import nn
import torch.nn.functional as F

class MLP(nn.Module):
    def __init__(self, dim, embedding_size=256, hidden_size=2048, batch_norm_mlp=False):
        super().__init__()
        norm = nn.BatchNorm1d(hidden_size) if batch_norm_mlp else nn.Identity()
        self.net = nn.Sequential(
            nn.Linear(dim, hidden_size),
            norm,
            nn.ReLU(inplace=True),
            nn.Linear(hidden_size, embedding_size)
        )

    def forward(self, x):
        return self.net(x)

class AddProjHead(nn.Module):
    def __init__(self, model, in_features, layer_name, hidden_size=4096, embedding_size=256, batch_norm_mlp=True):
        super(AddProjHead, self).__init__()
        self.backbone = model
        setattr(self.backbone, layer_name, nn.Identity())
        self.backbone.conv1 = torch.nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1, bias=False)
        self.backbone.maxpool = torch.nn.Identity()
        self.projection = MLP(in_features, embedding_size, hidden_size=hidden_size, batch_norm_mlp=batch_norm_mlp)

    def forward(self, x, return_embedding=False):
        embedding = self.backbone(x)
        if return_embedding:
            return embedding
        return self.projection(embedding)

The BYOL Training Process

With the architecture in place, we can now implement the BYOL training process. The following code outlines the core components of the BYOL module, including the student and teacher networks, and the forward pass:

class BYOL(nn.Module):
    def __init__(self, net, batch_norm_mlp=True, layer_name='fc', in_features=512, projection_size=256, projection_hidden_size=2048, moving_average_decay=0.99, use_momentum=True):
        super().__init__()
        self.net = net
        self.student_model = AddProjHead(model=net, in_features=in_features, layer_name=layer_name, embedding_size=projection_size, hidden_size=projection_hidden_size, batch_norm_mlp=batch_norm_mlp)
        self.use_momentum = use_momentum
        self.teacher_model = self._get_teacher()
        self.target_ema_updater = EMA(moving_average_decay)
        self.student_predictor = MLP(projection_size, projection_size, projection_hidden_size)

    @torch.no_grad()
    def _get_teacher(self):
        return copy.deepcopy(self.student_model)

    @torch.no_grad()
    def update_moving_average(self):
        assert self.use_momentum, 'you do not need to update the moving average, since you have turned off momentum for the target encoder'
        assert self.teacher_model is not None, 'target encoder has not been created yet'
        for student_params, teacher_params in zip(self.student_model.parameters(), self.teacher_model.parameters()):
            old_weight, up_weight = teacher_params.data, student_params.data
            teacher_params.data = self.target_ema_updater.update_average(old_weight, up_weight)

    def forward(self, image_one, image_two=None, return_embedding=False):
        if return_embedding or (image_two is None):
            return self.student_model(image_one, return_embedding=True)
        student_proj_one = self.student_model(image_one)
        student_proj_two = self.student_model(image_two)
        student_pred_one = self.student_predictor(student_proj_one)
        student_pred_two = self.student_predictor(student_proj_two)
        with torch.no_grad():
            teacher_proj_one = self.teacher_model(image_one).detach_()
            teacher_proj_two = self.teacher_model(image_two).detach_()
        loss_one = loss_fn(student_pred_one, teacher_proj_one)
        loss_two = loss_fn(student_pred_two, teacher_proj_two)
        return (loss_one + loss_two).mean()

Results: KNN Accuracy vs. Pretraining Epochs

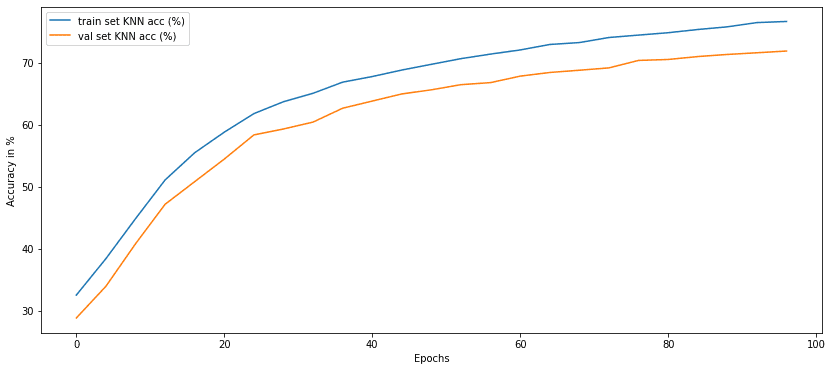
After implementing BYOL, we can evaluate its performance by measuring KNN accuracy over the course of training. The results indicate that BYOL can achieve a validation accuracy of approximately 70% on the CIFAR-10 dataset after 100 epochs, demonstrating the effectiveness of the method in learning meaningful representations without any labels.

Conclusion

BYOL represents a significant advancement in self-supervised learning, showcasing the potential of learning representations without relying on negative samples. By focusing on positive pairs and leveraging an asymmetric architecture, BYOL effectively minimizes the distance between augmented views of the same image, leading to impressive performance on various tasks.

As the field of self-supervised learning continues to evolve, methods like BYOL pave the way for more efficient and effective learning paradigms, enabling the development of robust models that can operate in real-world scenarios without the need for extensive labeled datasets.

For those interested in further exploring self-supervised learning, consider checking out additional resources and tutorials on the topic. Your support through social media sharing, donations, or purchasing related literature is greatly appreciated as we continue to advance the understanding of deep learning techniques.