Exploring Graph Neural Networks: A New Frontier in Deep Learning

In the realm of deep learning, traditional datasets have predominantly been represented in Euclidean space, particularly in applications like computer vision and natural language processing (NLP). However, as the complexity of data increases, there is a growing recognition of non-Euclidean data, particularly those represented as graphs. This shift has led to the emergence of Graph Neural Networks (GNNs), a powerful framework designed to apply deep learning techniques to graph-structured data.

Understanding Graph Neural Networks

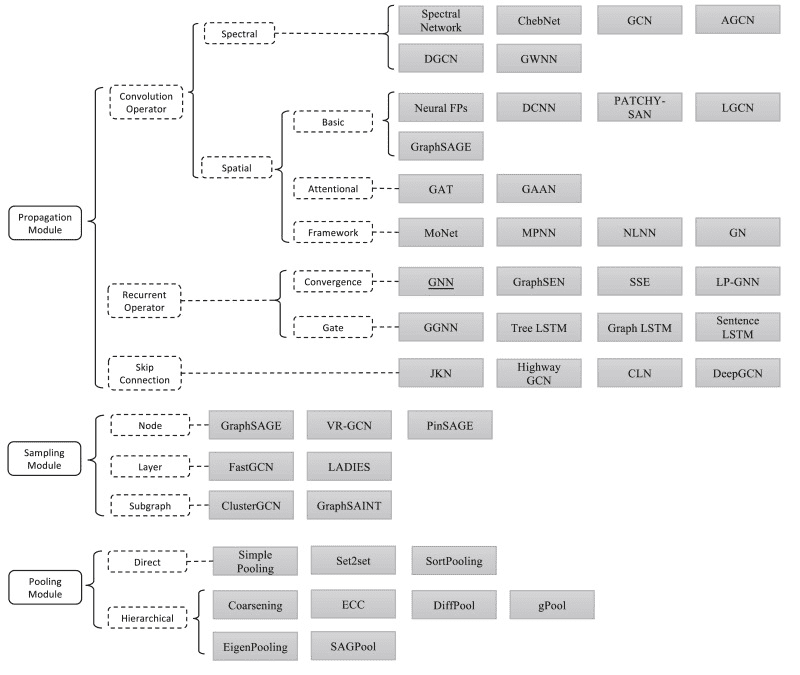
Graph Neural Networks are not a single architecture but rather a collection of various algorithms aimed at processing graph data. The term "GNN" encompasses a wide range of models, each with unique characteristics and applications. A recent review by Zhou et al. provides a comprehensive overview of the most significant papers in the field, illustrating the diversity and evolution of GNN architectures.

Basic Principles of Graphs

To delve deeper into GNNs, it’s essential to understand some fundamental principles and notation associated with graphs. A graph consists of a set of nodes (or vertices) and edges (connections between nodes). Both nodes and edges can have associated features. For instance, a node’s feature vector is denoted as ( hi ), where ( i ) is the node’s index, while an edge’s feature vector is represented as ( e{ij} ), where ( i ) and ( j ) are the nodes connected by the edge.

Graphs can be directed or undirected, weighted or unweighted, which means that different GNN architectures may be tailored to specific types of graphs or designed to handle all variations.

The Concept of Graph Convolution

At the heart of most GNN architectures lies the concept of graph convolution. This approach generalizes the idea of convolution from images to graphs. In essence, graph convolution predicts the features of a node in the next layer based on the features of its neighboring nodes. This transformation allows for the creation of latent feature representations that can be utilized for various tasks.

Mathematically, the transformation can be expressed as:

[ x_i \rightarrow h_i ]

where ( x_i ) represents the node’s features, and ( h_i ) represents the transformed features in a latent space.

Applications of Graph Convolution

The latent node feature vectors generated through graph convolution can be employed in several applications, typically falling into one of three categories:

1. Node Classification: By applying a shared function ( f ) to each latent vector ( h_i ), predictions can be made for each node, classifying them based on their features.

   [ Z_i = f(h_i) ]

2. Edge Classification: Similar to node classification, edges can be classified based on their features, requiring both adjacent node vectors and edge features.

   [ Z_{ij} = f(h_i, hj, e{ij}) ]

3. Graph Classification: This involves predicting attributes for entire graphs by aggregating all node features and applying an appropriate function.

   [ Z_G = f\left(\sum_i h_i\right) ]

The aggregation function is typically permutation-invariant, such as summation, mean, or pooling operations.

Inductive vs. Transductive Learning

A crucial distinction in GNN literature is between inductive and transductive learning.

• Transductive Learning: The model encounters both training and test data during training. If new nodes are added to the graph, the model must be retrained.

• Inductive Learning: The model is trained only on the training data and can generalize to unseen data. For instance, in a graph with 10 nodes, if 6 are used for training and 4 for testing, the model can learn to predict labels for the test nodes without having seen them during training.

GNN Architectures: A Closer Look

Spectral Methods

Spectral methods operate in the spectral domain of graphs, utilizing graph signal processing techniques. The convolution operator is defined using the Fourier transform, allowing for operations in the spectral domain. However, these methods can be computationally inefficient for large graphs.

1. Spectral Networks: These reduce the filter in the spectral domain to a diagonal matrix, but they lack locality, as the filter is applied across the entire graph.

2. ChebNets: To address locality, ChebNets propose that feature representation should only be influenced by a node’s ( k )-hop neighborhood, significantly reducing computational complexity.

3. Graph Convolutional Networks (GCN): GCNs simplify ChebNets by enforcing self-connections and using symmetric normalization of the Laplacian, making them one of the most widely used GNN architectures.

Spatial Methods

Spatial methods define convolutions directly on the graph based on its topology. They typically involve transforming node feature vectors, aggregating them, and updating each node’s feature vector based on its neighbors.

1. Message Passing Neural Networks (MPNN): MPNNs introduce the concept of messages, allowing nodes to send and receive information across edges. This architecture is flexible but can face scalability challenges.

2. Graph Attention Networks (GAT): GATs enhance the message-passing framework by incorporating an attention mechanism, allowing the model to weigh the importance of neighboring nodes dynamically.

Sampling Methods

To tackle scalability issues, sampling methods have been introduced. Instead of using all neighborhood information, these methods sample a subset of neighbors for propagation.

1. GraphSAGE: This framework samples nodes from the neighborhood, aggregates their features, and performs classification. It allows for efficient training on large graphs.

2. PinSAGE: An extension of GraphSAGE, PinSAGE is designed for large-scale applications, such as recommendation systems, leveraging random walks to define node neighborhoods.

Dynamic Graphs

Dynamic graphs, which change over time, present unique challenges. Temporal Graph Networks (TGN) are a promising architecture that captures the evolving nature of graphs, allowing for predictions based on temporal neighborhoods.

Conclusion

Graph Neural Networks represent a vibrant and rapidly evolving field with immense potential. As more datasets in real-world applications are structured as graphs, the relevance of GNNs will only continue to grow. Future explorations will utilize frameworks like PyTorch Geometric to build and experiment with GNN architectures.

For those interested in delving deeper into this exciting area, resources such as lectures by Petar Veličković and video series by Aleksa Gordić provide excellent starting points. As we continue to explore the capabilities of GNNs, the possibilities for innovation and application are boundless.

If you find this exploration of GNNs valuable, consider supporting further research and writing in this field. Together, we can unlock the full potential of graph-based deep learning.