Unveiling Neural Arithmetic Logic Units (NALU): A New Frontier in Deep Learning

In the rapidly evolving landscape of artificial intelligence, every new release from DeepMind generates a wave of excitement and anticipation. Following the monumental success of AlphaGo, which defeated the world’s top Go player, the AI community eagerly awaits each new paper from this pioneering research group. Recently, DeepMind published a groundbreaking paper titled Neural Arithmetic Logic Units (NALU), which promises to address a significant limitation in traditional neural networks. This article delves into the essence of NALUs, their necessity, functionality, and practical applications, along with a hands-on implementation guide.

Why We Need NALUs

Neural networks have demonstrated an extraordinary ability to learn complex functions across various data types, including numbers, images, and sounds. However, they possess a critical flaw: they struggle with counting and extrapolating values beyond their training range. For instance, if a neural network is trained on a dataset ranging from 0 to 100, it will only output values within that same range. This limitation poses challenges when attempting to build models that require counting or extrapolating beyond the observed data.

Consider a scenario where we train a neural network with the input data [0, 1, 2, 3, 4, 5]. If we expect it to output 6, we are likely to be disappointed. The graph below illustrates this limitation, showing how the mean error increases significantly for values outside the training range.

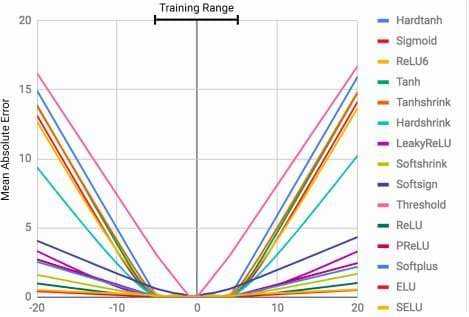
What is NALU?

Enter Neural Arithmetic Logic Units (NALUs), a novel solution designed to overcome the counting limitations of traditional neural networks. NALUs build upon the Neural Accumulator model (NAC), which is capable of performing linear transformations and accumulating inputs additively.

NALUs extend the functionality of NACs by incorporating both addition and multiplication capabilities. They consist of two NAC cells—one dedicated to addition and the other to multiplication—interpolated by a learned sigmoidal gate. This architecture allows NALUs to perform arithmetic operations more effectively, enabling them to represent complex mathematical functions.

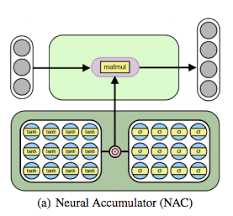
The intricate design of the gates in NALUs is rooted in advanced mathematical principles, making it a sophisticated tool for enhancing neural networks. The versatility of NALUs allows them to be integrated into various models, from convolutional networks to autoencoders, thereby improving their performance and extending their capabilities.

Practical Applications of NALUs

The authors of the NALU paper have explored several promising applications, including:

• Learning Simple Arithmetic Functions: NALUs can effectively learn and perform basic arithmetic operations.
• Counting Handwritten Characters: They can count the number of characters in an image, showcasing their utility in image processing tasks.
• Translating Text-Number Expressions: NALUs can convert textual representations of numbers into their numeric counterparts.
• Tracking Time in Grid-World Environments: They can be employed in reinforcement learning scenarios to track time and make decisions based on temporal data.

For a deeper understanding of these applications, readers are encouraged to explore the original paper.

Implementation in Python

To illustrate the power of NALUs, let’s implement one using TensorFlow and Python. With the mathematical foundations laid out in the paper, we can create a simple NALU and test its performance on arithmetic functions.

Step 1: Define the NALU Function

import tensorflow as tf
import numpy as np

def NALU(prev_layer, num_outputs):
    eps = 1e-7
    shape = (int(prev_layer.shape[-1]), num_outputs)
    W_hat = tf.Variable(tf.truncated_normal(shape, stddev=0.02))
    M_hat = tf.Variable(tf.truncated_normal(shape, stddev=0.02))
    W = tf.tanh(W_hat) * tf.sigmoid(M_hat)
    a = tf.matmul(prev_layer, W)
    G = tf.Variable(tf.truncated_normal(shape, stddev=0.02))
    m = tf.exp(tf.matmul(tf.log(tf.abs(prev_layer) + eps), W))
    g = tf.sigmoid(tf.matmul(prev_layer, G))
    out = g * a + (1 - g) * m
    return out

Step 2: Create Dummy Data

We will generate some dummy data to train and test our model. The training set will have a limited range, while the test set will have a broader range to evaluate the model’s extrapolation capabilities.

arithmetic_functions = {
    'add': lambda x, y: x + y,
}

def get_data(N, op):
    split = 4
    X_train = np.random.rand(N, 10) * 10
    a = X_train[:, :split].sum(1)
    b = X_train[:, split:].sum(1)
    Y_train = op(a, b)[:, None]

    X_test = np.random.rand(N, 10) * 100
    a = X_test[:, :split].sum(1)
    b = X_test[:, split:].sum(1)
    Y_test = op(a, b)[:, None]

    return (X_train, Y_train), (X_test, Y_test)

Step 3: Build and Train the Model

Now, we will set up the TensorFlow session, define the placeholders, and run the backpropagation algorithm.

tf.reset_default_graph()
train_examples = 10000
(X_train, Y_train), (X_test, Y_test) = get_data(train_examples, arithmetic_functions['add'])

X = tf.placeholder(tf.float32, shape=[train_examples, 10])
Y = tf.placeholder(tf.float32, shape=[train_examples, 1])
X_1 = NALU(X, 2)
Y_pred = NALU(X_1, 1)
loss = tf.nn.l2_loss(Y_pred - Y)
optimizer = tf.train.AdamOptimizer(0.1)
train_op = optimizer.minimize(loss)

with tf.Session() as session:
    session.run(tf.global_variables_initializer())
    for ep in range(50000):
        _, pred, l = session.run([train_op, Y_pred, loss], feed_dict={X: X_train, Y: Y_train})
        if ep % 1000 == 0:
            print('epoch {0}, loss: {1}'.format(ep, l))

    _, test_predictions, test_loss = session.run([train_op, Y_pred, loss], feed_dict={X: X_test, Y: Y_test})

print(test_loss)

The loss (mean square error) on the test set turns out to be remarkably low, demonstrating the model’s ability to extrapolate effectively beyond the training data.

Conclusion

The introduction of Neural Arithmetic Logic Units (NALU) marks a significant advancement in the capabilities of neural networks. By enabling models to perform arithmetic operations and extrapolate beyond their training data, NALUs open up new avenues for research and application in various fields, from computer vision to natural language processing. As we continue to explore the potential of NALUs, it is clear that their integration into existing models can enhance performance and broaden the scope of deep learning applications.

For those interested in deepening their understanding of deep learning, consider exploring the book Deep Learning in Production, which provides insights into building, training, deploying, and maintaining deep learning models.

Learn more about the book here.

Disclosure: Please note that some of the links above might be affiliate links, and at no additional cost to you, we will earn a commission if you decide to make a purchase after clicking through.